How to Calculate SMAPE in Python

The Symmetric mean absolute percentage error (SMAPE or sMAPE) is used to measure accuracy based on percentage errors for dataset. We will discuss about SMAPE formula, create SMAPE function in python, examples on SMAPE in python and SMAPE error.

SMAPE is expressed as a percentage. SMAPE has both a lower and an upper bound. The range of the SMAPE function results between 0% to 200%.

In this article, we will discuss about how calculate SMAPE in python and SMAPE error.

SMAPE Formula

The symmetric mean absolute percentage error (SMAPE) is defined as follows:

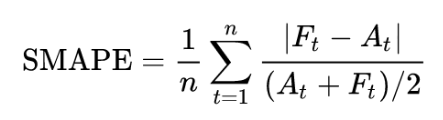
Where,

A_t = is actual value
F_t = is forecast value
n = number of points in samples

We will be using numpy library to generate actual and forecast arrays. As there is no in built function in python to calculate SMAPE, we will write custom function for SMAPE calculation using smape formula in python.

Cool Tip: Learn how to calculate mean squared error (MSE) in python!

pip install numpy

If you don’t have numpy package installed on your system, use below command in command prompt

pip install numpy

How to calculate SMAPE in python

Let’s understand about how to calculate symmetric mean absolute percentage error (SMAPE) in python with given below code

import numpy as np

def smape(act,forc):
    return 100/len(act) * np.sum(2 * np.abs(forc - act) / (np.abs(act) + np.abs(forc)))

#define Actual and forecast data array

actual = np.array([10,11,12,12,14,18,20])

forecast = np.array([9,10,13,14,17,16,18])

# Calculate SMAPE

result = smape(actual,forecast)

# print the result

print("SMAPE :",result)

In the above example, we have created actual and forecast array using numpy package array function.

Our custom python function smape() having smape formula implementation accepts act and forc as input parameters which are actual and forecast array and return SMAPE result.

Above python code gives Symmetric mean absolute percentage error (SMAPE) for given actual and forecast dataset is 12.15437%

Cool Tip: Learn how to calculate root mean squared error (RMSE) in python!

Example 1 – SMAPE Calculation

Lets assume we have actual and forecast dataset as below

actual = [4,7,3,9,12,8,14,10,12,12]

forecast = [5,7,3,8,10,8,12,11,11,13]

Calculate SMAPE for given model.

Here, again we will using numpy package to create actual and forecast array and custom smape() function for SMAPE calculation in python code as below

SMAPE in Python Code

import numpy as np
# Create smape function as per SMAPE formula
def smape(act,forc):
    return 100/len(act) * np.sum(2 * np.abs(forc - act) / (np.abs(act) + np.abs(forc)))

#define Actual and forecast data array

actual = np.array([4,7,3,9,12,8,14,10,12,12])

forecast = np.array([5,7,3,8,10,8,12,11,11,13])

# Calculate SMAPE

result = smape(actual,forecast)

# print the result

print("SMAPE :",result)

Above python code gives Symmetric mean absolute percentage error (SMAPE) for given actual and forecast dataset is 9.37728%

Cool Tip: Know more about how to autocorrelation in python!

Example 2 – SMAPE Calculation (Upper limit hit)

Lets consider a case where one of the actual dataset or forecast dataset has 0 value,

Here, for example we will use actual = [0] and forecast = [5]

Using below python code, lets calculate SMAPE using custom SMAPE function created using above given SMAPE formula.

SMAPE in Python Code

import numpy as np

# Create smape function with SMAPE formula
def smape(act,forc):
    return 100/len(act) * np.sum(2 * np.abs(forc - act) / (np.abs(act) + np.abs(forc)))

#define Actual and forecast data array

actual = np.array([0])

forecast = np.array([5])

# Calculate SMAPE

result = smape(actual,forecast)

# print the result

print("SMAPE :",result)

Above code gives Symmetric mean absolute percentage error (SMAPE) for given actual and forecast dataset is 200% . As actual forecast value is 0, hence SMAPE hits upper limit of error i.e.. 200%

Cool Tip: Know more about how to calculate MAPE in python!

Conclusion

I hope, you may have liked the above tutorial on how to calculate SMAPE in python. Few other points to remember while using SMAPE for time series forecasting is, sMAPE can take negative values, so interpretation of “absolute percentage error” can be misleading.

If the actual value or forecast value is 0, the value of error will hit upper limit of error i.e.. 200%.