How to Calculate MAPE in Python

The mean absolute percentage error (MAPE) or mean absolute percentage deviation (MAPD) is used to measure prediction accuracy for a forecasting method in statistics.

Mean absolute percentage error (MAPE) is used as loss function in regression problems. Its very easy to interpret and understand as it explain the error in terms of percentages.

In this tutorial, we will discuss about how to calculate MAPE in python.

MAPE Formula

The mean absolute percentage error (MAPE) measures the accuracy as a ratio given by MAPE formula as below:

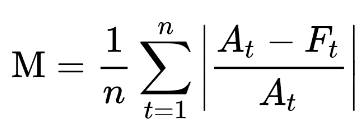
Where,

M = mean absolute percentage error (MAPE)
n = sample size
A_t = actual value
F_t = forecast value

We will be using numpy package to generate actual and forecast arrays. As there is no in-built function available MAPE calculation in python, we will write a custom function based on the given MAPE formula.

pip install numpy

If you don’t have numpy package installed on your system, use below command in command prompt

pip install numpy

How to Calculate MAPE in Python

Let’s understand how to calculate the mean absolute percentage error (MAPE) with given below python code

import numpy as np

def mape(actual,pred):
    return np.mean(np.abs((actual - pred) / actual)) * 100

actual = np.array([10,11,12,12,14,18,20])
pred = np.array([11,13,14,14,15,16,18])

#Calculate the MAPE
result = mape(actual,pred)

#print the result

print("The mean absolute percentage error: ",result)

In the above example, we have created actual and prediction array using numpy library array function.

using above mape formula in python, we have created custom python function mape() accepts actual and pred as input parameters and returns MAPE result.

Above code gives Mean absolute percentage error (MAPE) for given actual and prediction dataset is 12.82415%

Example 1 – MAPE Calculation

Let’s assume we have actual and forecast dataset as below

actual = [4,7,3,9,12,8,14,10,12,12]
forecast = [5,7,3,8,10,8,12,11,11,13]

Calculate MAPE prediction accuracy for given model.

Here, again we will be using numpy library array function to create actual and forecast array as given in problem statement.

custom mape() function for MAPE calculation in python code is given as below:

import numpy as np

def mape(actual,pred):
    return np.mean(np.abs((actual - pred) / actual)) * 100

actual = np.array([4,7,3,9,12,8,14,10,12,12])
pred = np.array([5,7,3,8,10,8,12,11,11,13])

#Calculate the MAPE
result = mape(actual,pred)

#print the result

print("The mean absolute percentage error: ",result)

In the above python code, we have created custom mape() function using mape formula. It access actual and pred array and return mean absolute percentage error (MAPE) for given model is 9.37301%

Example 2 – MAPE Calculation ( Actual = 0)

Let’s consider a case where we have an actual and forecast dataset and actual data has 0 value

For example, actual = [0,0,0,0,0] and forecast = [0,1,1,2,1]

If we try to calculate MAPE with above actual and forecast dataset points, it will not calculate as actual = 0 which results in divide by zero error during calculation.

This is one of the drawbacks of the MAPE, if actual values are zero, it will results in undefined.

Conclusion

I hope you may have liked above tutorial on how to calculate MAPE in python educational and helpful.

As discussed in above examples, it is used to measure prediction accuracy for the forecast model. If the MAPE value is less it means there is less error between actual and forecast model, results in more accuracy.

It has few drawbacks as discussed in example 2, if actual dataset is having 0 values, MAPE can not be calculated because of divide by zero error.

Another drawback is, MAPE is asymmetric, it puts heavier penalty on negative errors when A_t < F_t ( Forecast value are higher than actual) than on positive errors. It means that If Actual value are higher than forecast, percentage error can not exceed 100%, however, if forecast value are too high than actual, percentage error exceeds 100%