How to Calculate Mean Squared Error (MSE) in Python

Mean squared error (MSE) of an estimator measures the average of the squared errors, it means averages squared difference between the actual and estimated value.

MSE is almost positive because MSE of an estimator does not account for information that could produce more accurate estimate.

In statistical modelling, MSE is defined as the difference between actual values and predicted values by the model and used to determine prediction accuracy of a model.

In this tutorial, we will discuss about how to calculate mean squared error (MSE) in python.

Mean Squared Error Formula

The mean squared error (MSE) formula is defined as follows:

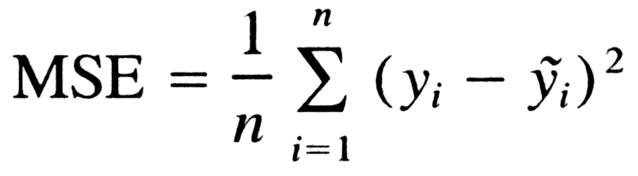
Where,

n = sample data points
y – actual size
y^ – predictive values

MSE is the means of squares of the errors ( yi – yi^)².

We will be using numpy library to generate actual and predication values.

As there is no in built function available in python to calculate mean squared error (MSE), we will write simple function for calculation as per mean squared error formula.

pip install numpy

If you don’t have numpy package installed on your system, use below command in command prompt

pip install numpy

How to Calculate MSE in Python

Lets understand with examples about how to calculate mean squared error (MSE) in python with given below python code

import numpy as np

def mse(actual,prediction):
    return np.square(np.subtract(actual,prediction)).mean()

#define Actual and Prediction data array

actual = np.array([10,11,12,12,14,18,20])
pred = np.array([9,10,13,14,17,16,18])


#Calculate MSE

result = mse(actual,pred)

#print the result

print("Mean squared error (MSE) :", result)

In the above example, we have created actual and prediction array with the help of numpy package array function.

We have written simple function mse() as per mean squared error formula which takes two parameters actual and prediction data array. It calculates mean of the squares of (actual – prediction) using numpy packages square and mean function.

Above code returns mean squared error (MSE) value for given actual and prediction model is 3.42857

Lets check out Mean squared Error (MSE) calculation with few other examples

Info Tip: How to calculate SMAPE in Python!

Example 1 – Mean Squared Error Calculation

Lets assume we have actual and forecast dataset as below

actual = [4,7,3,9,12,8,14,10,12,12]

prediction = [5,7,3,8,10,8,12,11,11,13]

Calculate MSE for given model.

Here, again we will be using numpy package to create actual and prediction array and simple mse() function for mean squared error calculation in python code as below

import numpy as np

def mse(actual,pred):
    return np.square(np.subtract(actual,pred)).mean()

#define Actual and Prediction data array

actual = np.array([4,7,3,9,12,8,14,10,12,12])
pred = np.array([5,7,3,8,10,8,12,11,11,13])


#Calculate MSE

result = mse(actual,pred)

#print the result

print("Mean squared error (MSE) :", result)

Above code returns mean squared error (MSE) for given actual and prediction dataset is 1.3

Info Tip: How to calculate rolling correlation in Python!

Example 2 – Mean Squared Error Calculation

Lets take another example with below actual and prediction data values

actual = [-2,-1,1,4]
prediction = [-3,-1,2,3]

Calcualte MSE for above model.

Using below python code, lets calculate MSE

import numpy as np

def mse(actual,pred):
    return np.square(np.subtract(actual,pred)).mean()

#define Actual and Prediction data array

actual = np.array([-2,-1,1,4])
pred = np.array([-3,-1,2,3])


#Calculate MSE

result = mse(actual,pred)

#print the result

print("Mean squared error (MSE) :", result)

Above code returns mean squared error (MSE) for given actual and prediction dataset is 0.75. It means it has less squared error and hence this model predicts more accuracy.

Info Tip: How to calculate z score in Python!

Conclusion

I hope, you may find how to calculate MSE in python tutorial with step by step illustration of examples educational and helpful.

Mean squared error (MSE) measures the prediction accuracy of model. Minimizing MSE is key criterion in selecting estimators.