How to Calculate Root Mean Squared Error (RMSE) in Python

The root mean squared error (RMSE) is used to measured the differences between values predicted by the model and observed values of the model.

The root mean squared error (RMSE) is always non-negative, RMSE value near to 0 indicates a perfect fit to the data.

Root mean squared error or Root mean squared deviation (RMSD) is the square root of the average of squared errors. RMSD is measure of accuracy to compare forecasting errors of different models for a particular dataset.

In this tutorial, we will discuss about how to calculate root mean squared error (RMSE) in python.

RMSE Formula

The root mean squared error (RMSE) is defined as follows:

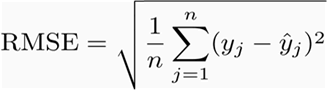
Where,

n = sample data points
y = predictive value for the j^th observation
y^ = observed value for j^th observation

For an unbiased estimator, RMSD is square root of variance also known as standard deviation. RMSE is the good measure for standard deviation of the typical observed values from our predicted model.

We will be using sklearn.metrics library available in python to calculate mean squared error, later we can simply use math library to square root of mean squared error value.

We will be using numpy library to generate actual and predication array.

pip install numpy

If you don’t have numpy package installed on your system, use below command in command prompt

pip install numpy

pip install sklearn

If you don’t have sklearn package installed on your system, use below commands in command prompt

pip install sklearn

How to Calculate RMSE in Python

Lets understand with examples about how to calculate RMSE in python with given below python code

from sklearn.metrics import mean_squared_error
from math import sqrt
import numpy as np

#define Actual and Predicted Array

actual = np.array([10,11,12,12,14,18,20])

pred = np.array([9,10,13,14,17,16,18])

#Calculate RMSE

result = sqrt(mean_squared_error(actual,pred))

# Print the result

print("RMSE:", result)

In the above example, we have created actual and prediction array with the help of numpy package array function.

We then use mean_squared_error() function of sklearn.metrics library which take actual and prediction array as input value. It returns mean squared error value.

Later, we find RMSE value using square root of mean squared error value.

Above code returns root mean squared error (RMSE) value for given actual and prediction model is 1.85164

Lets check out root mean squared value (RMSE) calculation with few more examples.

Example 1 – RMSE Calculation

Lets assume, we have actual and predicted dataset as follows

actual = [4,7,3,9,12,8,14,10,12,12]

prediction = [5,7,3,8,10,8,12,11,11,13]

Calculate RMSE for given model.

Here, again we will be using numpy package to create actual and prediction array and mean_squared_error() funciton of sklearn.metrics library for RMSE calculation in python.

Python code is given as below

from sklearn.metrics import mean_squared_error
from math import sqrt
import numpy as np

#define Actual and Predicted Array

actual = np.array([4,7,3,9,12,8,14,10,12,12])

pred = np.array([5,7,3,8,10,8,12,11,11,13])

#Calculate RMSE

result = sqrt(mean_squared_error(actual,pred))

# Print the result

print("RMSE:", result)

Above code returns root mean squared (RMSE) for given actual and prediction dataset is 1.14017

Example 2 – RMSE Calculation

Lets assume, we have actual and predicted dataset as follows

actual = [14,17,13,19,12,18,14,10,12,12]

prediction = [15,14,14,18,10,16,12,11,11,13]

Calculate RMSE for given model.

Here, again we will be using numpy package to create actual and prediction array and mean_squared_error() funciton of sklearn.metrics library for RMSE calculation in python.

Python code is given as below

from sklearn.metrics import mean_squared_error
from math import sqrt
import numpy as np

#define Actual and Predicted Array

actual = np.array([14,17,13,19,12,18,14,10,12,12])

pred = np.array([15,14,14,18,10,16,12,11,11,13])

#Calculate RMSE

result = sqrt(mean_squared_error(actual,pred))

# Print the result

print("RMSE:", result)

Above code returns root mean squared (RMSE) for given actual and prediction dataset is 1.643167

Conclusion

I hope, you may find how to calculate root mean square (RMSE) in python tutorial with step by step illustration of examples educational and helpful.

RMSE is mostly used to find model fitness for given dataset. If RMSE has value 0, it means that its perfect fit as there is no difference in predicted and observed values.